Foundations of quantum mechanics
What is truly quantum? How do we determine if a system behaves quantum mechanically? Despite their apparent innocence, these questions are deeply rooted into the foundations of quantum mechanics and address a broad spectrum of topics, from quantum correlations to non-commutativity of quantum operators, from “spooky actions at distance” to the interaction between a quantum system and the world that surrounds it. We are engaged into an extensive investigation on the ways quantumness manifests itself in systems of a variegate nature and complexity. Our tools are embodied by sophisticated ways in which correlations of a non classical nature are set and behave or “disturbance” over the configuration of a quantum system occur upon the performance of operations defies any expectation based on classical mechanics.
-
- Non-locality of mixed continuous-variable systems: There is life beyond the qubit! Harmonic oscillators embody an interesting battle-field for the development of a reliable technology based on quantum mechanics. Light, indeed, whose physics is not at all different from that of a harmonic oscillator (nevermind the mass!), is the prototype of a continuous variable: its quadratures operators (the phase-space analogues of position and momentum for a harmonic oscillator) have a continuous and unbounded spectrum. We study the manifestations of non-locality in multipartite mixed states of continuous-variable systems embodied, for instance, by light fields. We are looking for ways to impart non-local properties to the joint state of a many-mode system under the conditions of strong mixedness (due, for instance, to high local temperature), and to detect it by means of non-demanding measurements and local operations. We use both Bell’s and Svetlichny’s inequality to test the non-local character of the states that we engineer.
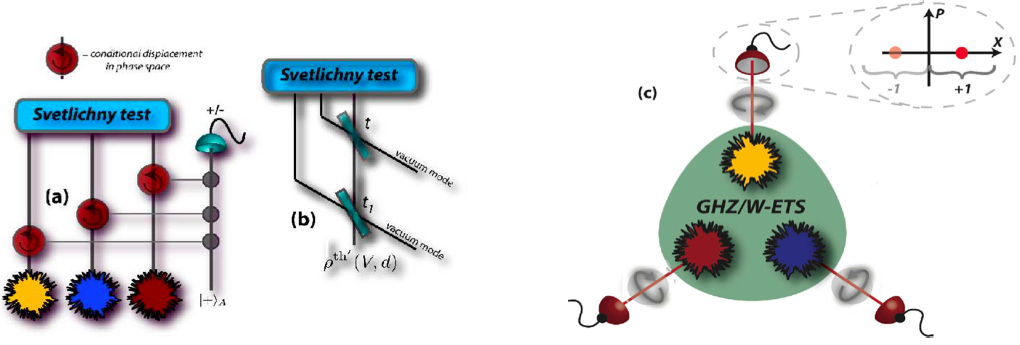
http://link.aps.org/doi/10.1103/PhysRevLett.102.060403
The formulation of (multipartite) non-locality tests is based on two assumptions of classical plausibility: locality (nothing done on particle A can have an influence on a lightcone-separated particle B) and realism (the outcomes of a measurement performed on one of the properties of a particle is pre-determined). When a (generalised) Bell’s inequality is violated, these assumptions (or one of them, although: which one?!) are not fulfilled. In 2003, Nobel laureate Tony Leggett formulated a model that basically gives up on locality to retain realism. This constraints the value that a particular combination of two-point correlation functions can take, should the locality assumption be satisfied by the classically realistic state of a system. Achieving values beyond such constraints falsifies Leggett’s model and witnesses non-local realism. We have designed a test for continuous-variable non-local realism and studied deeply the modifications that the unbounded nature of the spectrum of a continuous-variable system have on the classical bound to correlations, therefore extending Leggett’s argument to a domain unexplored before our endeavours.
- System-environment correlations and the implications for non-Markovianity: Why do not we observe quantum effects in our daily life? Why is it so difficult to make quantum features that have been enforced in the state of a system endure in time? An answer comes for the theory of so-called decoherence: the unavoidable interaction between a system and the world that surrounds it is quite out of control The environment is too large to keep track of it. If it is the dynamics of the system alone that we are interested in, the environment should be traced out, which has the effective result of spoiling the state of the system and make it only weakly quantum. The way this process occurs is still not fully understood, and a variegate phenomenology of such mechanism is in place. In a very coarse-grained manner, two categories of system-environment dynamics can be identified: the first assumes a rigid environmental system, immutable in its configuration and only weakly coupled to the system of interest. These assumptions typically give rise to what is called a “Markovian” evolution. In the second category, on the other hand, the environment is a dynamical system able to kick-back information that the system has poured into it and, thus, to get correlated to the system in a quantum mechanical way. As such, the system-environment evolution cannot be chopped into mutually independent “slices”, but the dynamics should be considered as a whole. Such mechanisms, which are commonly dubbed as “non-Markovian”, are largely unexplored and poorly understood.We are interested in the reasons behind the occurrence of non-Markovian dynamics and, in particular, the role played by system-environment correlations in the violation of the conditions signalling Markovianity. We work on establishing quantitative relations between the changes induced in the state of an environment and the state-homogenizing nature of the system’s evolution. Our goal is to understand which is a genuine signature of non-Markovianity.
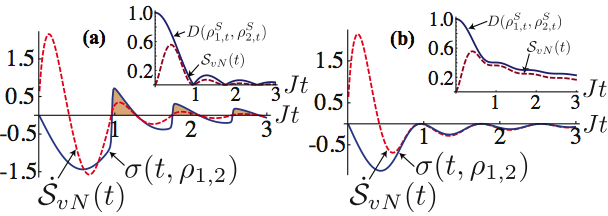 Our research in this context is also directed at the understanding of the features of open-system dynamics from the perspective of recent tools put forward for the quantification of the degree of non-Markovianity of a map. We use such tool in quantum many-body systems such as ultracold atoms and quantum spin chains. More details in our Many-Body Quantum Physics page!
Our research in this context is also directed at the understanding of the features of open-system dynamics from the perspective of recent tools put forward for the quantification of the degree of non-Markovianity of a map. We use such tool in quantum many-body systems such as ultracold atoms and quantum spin chains. More details in our Many-Body Quantum Physics page! - Quantum contextuality in continuous-variable systems:In quantum mechanics, two observables A and B are said to be compatible when the outcomes of a measurement of A performed on a system does not depend on any prior or simultaneous measurement of B. A set of mutually compatible observables defines a “context”, so that the above examples defines a situation where the measurement of A does not depend on the context or is “non-contextual”. Clearly, non-contextuality is a property inherent in the classical world. For quantum observables to assume such a property may at first hand seem reasonable. In fact, the Kochen-Specker (KS) theorem states that no non-contextual hidden variable theory can reproduce quantum mechanics. This is complementary to the Bell theorem and provides an equally viable tool to gaining insight into the open question to where exactly the boundary between the classical and quantum may lie. Kochen and Specker originally produced a set of observables associated with the squares of the components of the angular momentum operator along 117 different directions to demonstrate a contradiction with non-contextuality. Almost twenty five years later, Peres found a much simpler counter-example involving only six Pauli spin operators in the four-dimensional space of two spin-1/2 particles.
Peres’ formulation of the problem, however, is strictly dependent on the form of the state of the two particles. Mermin made a further simplification by extending the example to include three additional operators, thereby illustrating state-independence. The state-independent nature of the KS theorem is a rather distinctive feature: inequalities based on non-contextual hidden variable theories might be violated by any quantum state, regardless of their degree of entanglement. We study the falsification of non-contextuality inequalities in unbounded Hilbert spaces using a different viewpoint. In fact, while we keep the dichotomic structure of the observable entering the KS inequalities to test, we explicitly consider systems living in infinite-dimensional Hilbert spaces. In order to accomplish our goal, we take advantage of the well-known possibility to violate Bell-like inequalities using dichotomic non-Gaussian observables and continuous-variable systems prepared in quantum correlated Gaussian states as well as non-Gaussian states embedding a qubit state.
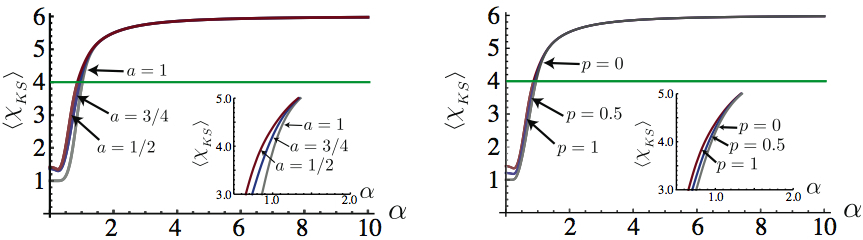
- Non-locality of mixed continuous-variable systems: There is life beyond the qubit! Harmonic oscillators embody an interesting battle-field for the development of a reliable technology based on quantum mechanics. Light, indeed, whose physics is not at all different from that of a harmonic oscillator (nevermind the mass!), is the prototype of a continuous variable: its quadratures operators (the phase-space analogues of position and momentum for a harmonic oscillator) have a continuous and unbounded spectrum. We study the manifestations of non-locality in multipartite mixed states of continuous-variable systems embodied, for instance, by light fields. We are looking for ways to impart non-local properties to the joint state of a many-mode system under the conditions of strong mixedness (due, for instance, to high local temperature), and to detect it by means of non-demanding measurements and local operations. We use both Bell’s and Svetlichny’s inequality to test the non-local character of the states that we engineer.