Quantum Many-body Physics
Our research in quantum many-body physics spans the following areas:
- Spin chains
In this context, we study the phase diagram of the bilinear-biquadratic model with a uniaxial field (single-ion anisotropy). This model is characterized by a rich phase diagram, shown in figure, containing different phases with distinctive features.
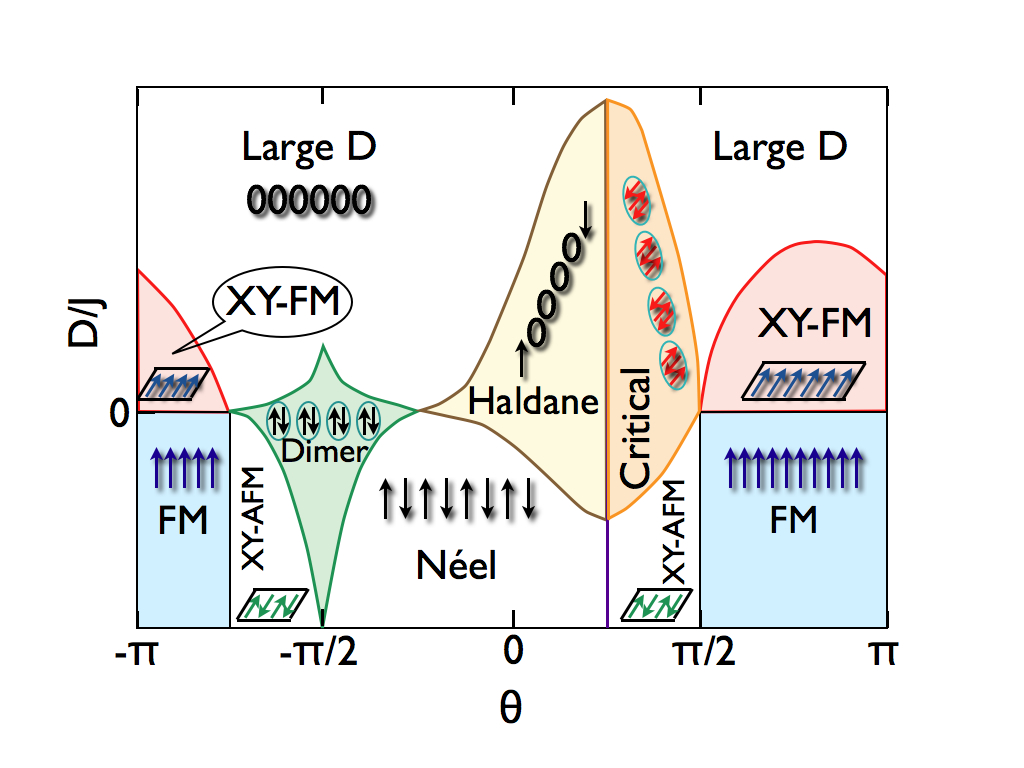
For example the system can be in a dimerized phase in which neighboring spins tend to pair in singlets and translational invariance is broken. A negative uniaxial field can also stabilize the nematic (XY-antiferromagnetic) and Neel phases in which rotational invariance is broken. For positive values of the uniaxial field the system is in a trivial gapped phase, the Large D phase, where the spins tend to the 0 component state. Finally, the model allows the celebrated Haldane phase, a topological gapped phase, characterized by a string order parameter, and containing the AKLT point. Such models can now be realized with ultracold atoms in optical lattices. In the section Quantum gases and ultracold atoms we discuss how to detect these phase using quantum polarization spectroscopy.
Further reading:
G. De Chiara, M. Lewenstein, A. Sanpera, Bilinear-biquadratic spin-1 chain undergoing quadratic Zeeman effectIt is now well established that entanglement between the two halves of a spin chain give a lot of information about the ground state of the system. For example, for critical points, it is known that the entanglement, as measured by the von Neumann entropy of the reduced density matrix of one of the two blocks, scales logarithmically with the size of the block. The prefactor is given by the central charge of the corresponding conformal field theory describing the critical point.
Another useful tool is the so called entanglement spectrum which can be related to the spectrum of the reduced density matrix of one of the two halves of a spin chain. It has been demonstrated by Pollmann et al., Phys. Rev. B 81, 064439 (2010), that the Haldane phase is uniquely characterised by a evenly degenerate entanglement spectrum, i.e. the eigenvalues of the reduced density matrix come always in even multiplets. We discovered that we can use the difference of the first two eigenvalues, called the Schmidt gap, to characterise the approaching of the Haldane phase from other phases. The Schmidt gap shows scaling behaviour in analogy to order parameters with the correct critical exponents, when going from the Neel to the Haldane phase. Similar results hold for the Ising model.
Further reading:
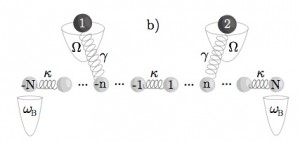
G. De Chiara, L. Lepori, M. Lewenstein, A. Sanpera, Entanglement Spectrum, Critical Exponents, and Order Parameters in Quantum Spin Chains, Phys. Rev. Lett. 109, 237208 (2012) - Entanglement generation in harmonic latticesEntanglement can be created between two non interacting particles if they are both interacting with a common environment. Here we consider two non interacting harmonic oscillators interacting with an environment formed by a one-dimensional array of harmonic oscillators.
We show that entanglement can be generated even when the two particles are further apart and even when the environment is initially at thermal equilibrium.
Further reading:
A. Wolf, G. De Chiara, E. Kajari, E. Lutz and G. Morigi, Entangling two distant oscillators with a quantum reservoir, Europhys. Lett. 95, 60008 (2011). - Coulomb crystalsWe study dynamical crossing of structural phase transitions in quasi-one-dimensional ion crystals. If the ions are confined to a plane, the crystal makes a transition from a linear to a planar zigzag structure (see below, left). When the ions are allowed to move in all three dimensions then a helical structure (somehow similar to DNA) can appear (see below, right). We study the statistics of the number of twists as a function of the speed in crossing the transition.

We study quantum superpositions of quantum states of ion crystals corresponding to different motional states (see figure below).
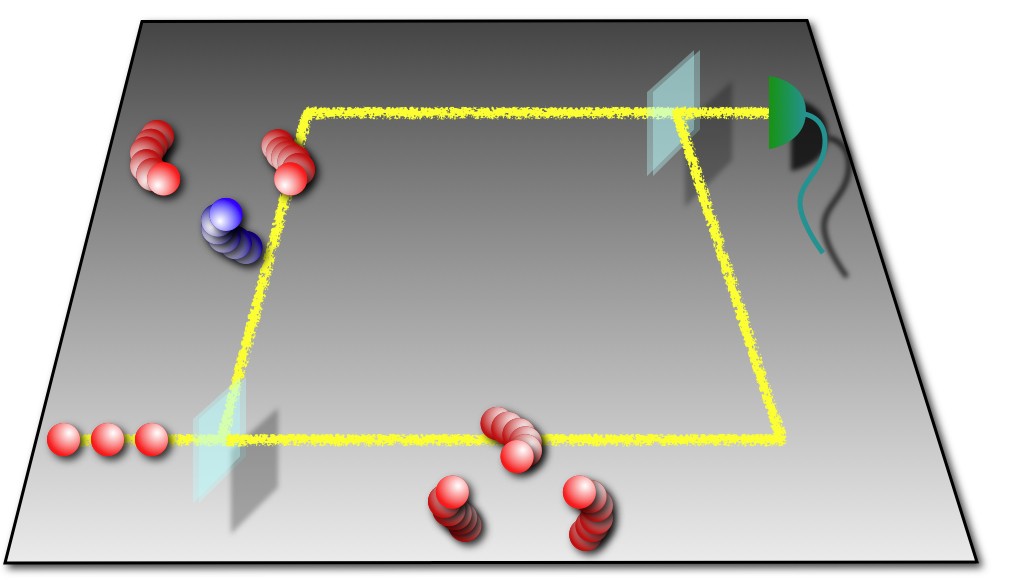
In particular we have proposed the way to detect superpositions of different crystalline structures with a Ramsey-type experiment using the internal state of one of the ions.
Further reading:
G. De Chiara, T. Calarco, S. Fishman, G. Morigi, Phys. Rev. A 78, 043414 (2008)J. D. Baltrusch, C. Cormick, G. De Chiara, T. Calarco, G. Morigi, Phys. Rev. A 84, 063821 (2011).
- Non-Markovianity in spin chainsWe study the dynamics of a qubit coupled to a spin environment via an energy-exchange mechanism. We show the existence of a point, in the parameter space of the system, where the qubit dynamics is effectively Markovian and that such a point separates two regions with completely different dynamical behaviors. Indeed, our study demonstrates that the qubit evolution can in principle be tuned from a perfectly forgetful one to a deep non-Markovian regime where the qubit is strongly affected by the dynamical back-action of the environmental spins. By means of quantum process tomography, we provide a complete and intuitive characterization of the qubit channel.
Further reading:
T. J. G. Apollaro, C. Di Franco, F. Plastina, M. Paternostro, Phys. Rev. A 83, 032103 (2011).